Introduction: Habitants with gardens often experience unpredictable growth and several solutions for/into life forms. Beside resting in a source sinc, e.g. a Black Hole or singularity, plants may benefit on energy equivalents for light, heat, water and nutrition.The nutrition equivalent, at rest, could partly be given by demolishing some roots of its own. In [1], it was found that small magnetic fields provide energy and rest into less growth; i.e. status quo.Another common way is staying in a group with other plants or behind larger. Then, they copy each other, or the large one, to remain and grow. Copying in a pot-arrangement is given in Figure 1.

Figure 1. Plants grown from seeds obtaining the same structure by copying each other. From top: Kamelia-type (Balsamina), Radish ‘Zlata’ and Cornflower (Centaurea cyanus) (photo of late spring event).
In the present paper, we will propose additional artificial devices for energy supply, based on theoretically modeling and homologies.
The models rely on light and optics, as a source of energy and energetic matter, and space itself, given by coordinates or areas.
1. Space-time and Optics
Optics is a branch of Physics and concerns gathering of light with man-made materials; typically lenses and other matter that preserve and alter the structure [2]. Light reveals in several formats, e.g. as hot-spots on a panel [3] or at Sea, and beams. For white-light beams, a spectral decomposition in a prism gives different colours at certain discrete angles. In the Solar System, an extrapolation gives that the Sun itself is a hot-spot.
Celestial bodies, e.g. planets, display angular symmetries e.g. spherical shapes around a rotational axis. Invoking rigid-body-mechanics an angle stems from angular velocity, denoted w. For a plane case, an angle v, dimensionless [4], is obtained by time integration of w, for a time scale with graininess [5]. In the present context, we will use the expression
w(t)=w0exp(re/r0 sin(fwot)) (0)
In 3 dimensions, the is defined as Q,tQT where Q is a matrix in SO(3), i.e. a rotation and/or a reflexion.
2. Reflexions and Aura
Sun Light can be gathered at a metallic Surface, c.f. Figure 2, and brings a certain Aura around it, described with e.g. w(t).
Remark. Another example, is a car with chrome finish. Light spots display and materialise not on the surface but a small distance above (the relecting origin). That might preveail over non-chrome to conquer rust.

Figure 2. Reflexion of light is beneficial adjacent to a plant since it contributes to an energy aura.
In (0), the values for f correspond to various shapes for a noncircular orbit (nco), e.g. f=2 has similarity with an ellips and f=3/2 relates to Mercury, the planet. At growth, such materialise in time [6], e.g. into the many petals of a flower, for larger f.
For planets, the eccentricity is limited compared with the radius of the circle (e.g. tidal waves and orbital ellipticy, f=2), but for other matter e.g. light plasma, other shapes are likely to occur. For example Liquid Helium, climbing up a wall may develop contact surface shapes with larger values for f to fit the surface structure.
3. Propulsion. Velocity for light.
Propulsion in free space, can be derived from the planetary motions and generalisation with a noncircular orbit. For a sidereal rotation with partial elongation at one side and relaxation at the other, described with f=1 in a nco, it is seen that the sidereal rotation may contribute to the orbital distance. This correspond to propulsion and may increase (e.g. the ‘translatory’ part of) the velocity.
Remark. The translation in this case is that with the largest curvature if the body remains in an orbital motion.
Theoretically, the elongation can be arbitrary large, and by that give a large velocity. For energetic matter
which are known to form individual continuum matter shapes, e.g. light plasma, that is likely to occur and brings an explanation for establishing ‘light velocity’ c, or a way for light to reach other points at a large distance.
4. Winds and Sun Breeze.
Close to water, there is a certain wind known as Sea Breeze. Other etymology for the phenomenon are
- Ocean Breeze, invoking the location
- Afternoon Breeze, remembering the time
- Sun Breeze, revealing the Primus Motor
A reason for the various names and recognitions, is the importance historically: The trades and other transportation in early days went by Sailing Ships.
Next, a description will be outlined and a homology is large photons interacting with other matter. Observation of Sun light on a water surface shows spots of Light moving towards the observer at land. The reaction on the water surface are waves that starts a wind adjacent, which then spreads in the atmosphere. It appears to be in weakly interaction with the observer i.e. not entirely objective, but to say that it could be elecitely induced by man is too much, because anything at land (or Sea) might be the target for the jumping spots.
Plausibly, a similar phenomenon occurs in a tree: On a sunny day, when walking next to semi-large trees with leaves, e.g. Asp, in a not so dense Frest, suddenly a motion starts from the leaves after which it increases fast, to obtain some more strength being able to bend also (at least) the smaller stems. The latter, as well as creation of Tornados invoves magnifcation in the atmosphere, as is known in meteorology. Also Sun Light is an input, since hot surface water add energy to a moving air parcel with interior angular velocity activity, e.g. so-called whirl-winds. In view of this, an artificial wind may provide energy to plants ( especially indoors, to mimic the outside climate).
5. Partial shade
In view of patterns and light-spots, partial shades mimic the leaves in a foliage, which in due course, time after time, may be copied into growth. Therefore some plants prefer growing together or below larger, and at occasions towards small hot-spots in a dense shadow.In another context, partial shade and hot- spot were analysed in conjunction with efficiency for a photovolatic panel [3].
6. A Black Hole in the center of the Garden
In the present context, we will analyse the location for small plants within other vegetation considered as a Black Hole.
A Model with Scharwzild geometry, gives that a radius of a black hole is given by R=2GM/c2
In a classical approach this may correspond to an object with a smaller mass and lower escape velocity and finite radius. Inside such an object, a densification into smaller sources developing outputs as strings will be evaluated:
Then, a radius could be small (from e.g. 2% of the main) and this corresponds to a large escape energy, which means that smaller objects, e.g. plants, will remain, as well as be able to profit on the energy in the hole, since being part in its density.
7. Continuum models and singularities for heat distributions from light
8.1.Introduction
Oscillations and traveling waves co-existing with a streamline flow, have been cast into modeling in various applications e.g. river flows, heat, EM and viscous flows [7].
In the present section, heat distributions from a source, will be modelled. The main factor giving the distribution is buoyancy [8,9] giving an upward flow of lighter heated air. With a wide shield, some heat can be gathered at suitable low locations. Other composed dynamic uplifts [10,11] or superimposed waves [12], give more complex fields or the details of classical buoyancy in a structural context.
Analytical quasi static solutions are related to results in FEM [13] for the symmetric case. The goal is to derive how heat layers and matter develop.
The content is organised into subsections: First, general models for heated particles are revisited. Then, calculus with differentials and couplings to a more solid boundary, will be proposed. Then, the real macro- scale heat distribution with buoyancy is considered. From that, conditions for singularities in a power representation are derived.
Reflexion is a main feature of light when interacting with matter, c.f. section 3 above. This generates discrete solution, since space consist of granular matter at certain scales [5]. In turn, discrete solutions provides quanta.
Singularities, as well as reflexions, are assumed to be sources for additional power in composed systems.
8.2. luid Dynamic Models and Quasistatic Heat
In fluid mechanics, the Bernoulli law (BL) is a governing balance when following the streamline of a Navier Stokes [14] flow. The equation reads
du2/2-dgh+p=const …………….. (1)
where d is density, u is velocity, g is gravity, h is a relative distance and p is the pressure.
With the preliminaries in [7], e.g. assuming that density d, depends on an internal variable proportional to velocity u, we obtain traveling waves. Super-position of exponential traveling waves gives solutions in terms of cosh() and sinh() ; i.e. hyperbolics.
The energy equation in continuum dynamics, gives Poisson’s equation, for a scalar temperature field (aka the heat equation), Figure 3. With generalisations into nonlinear parameters, internal friction and when input due to mechanical work, the balance equation changes. The additional terms are e.g. p(d,t/d) and n(u,x)2 where ,t denotes time differentiation and n is viscosity [15].
Depending on the sign of parameters (corresponding to linearisation of input/output), the equation is hyperbolic or elliptic, and the solutions are e.g. cosine hyperbolicus and cosine.

Figure 3. Geodesics for heat on the Stanford Bunny, from [16].
For the solid elastic case, a FEM-formulation [17] of the linear equation with boundary conditions, is solved numerically on a domain c.f. [13]. From the result in Figure 4, the temperature level might be traced as the sum of cosh() + const, for each direction (vertical and horisontal). Since lower in the centre, partly, the remote behaviour may be sufficiently described with a radial coordinate, r.
Remark. With a weak formulation, a singularity at r-dependency in polar coordinates is not always
regained, which means that a symmetric solution could be smooth also for that case.
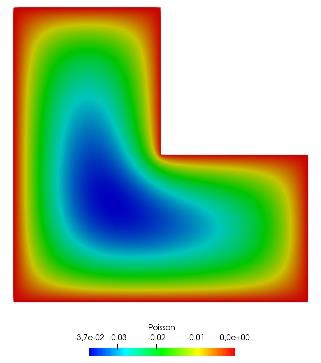
Figure 4. Temperature level for the heat equation; Poisson’s equation, with boundary conditions on input heat, [6]. Remark. In FEM, the Lagrangian element has an exact Gaussian integration, and other formats are e.g. serendipity elements.
8.3. Models for coupling to layers
In order to couple with material adjacent to air, we shall assume additional densities, parameters and pressure, (e.g. as sums with the air matter).
This admits:
-options for modeling layers without knowing the perpendicular radial velocity
-inputs to models with differential geometry (; convenient when matter appear as several d.o.fs)
-coupling between temperature and e.g. electricity in the static heat equation Adjacent to a plane boundary shield, a proposal for the gas law is : p= (d+dL+dE)(r+rL)H
where d is density, H is temperature, rL is an material parameter that changes with material layers and dL,
dE is additional density at layer or electricity. Here, we will consider a non-electric air layer close to matter such that
p=drLH ……………..(2)
With (2), a differentiation of BL (1), gives udu+drLH +rLdH =0 …..(3)
where du, drL and dH denotes differentials of the fields. This admits several kinds of solutions for temperature e.g. H~u and H~u2 . The latter is similar to that obtained in the original version (1), and has a certain symmetry.
Remark 1. Theoretically from the format (3), and assuming boundaries, it is seen that layer parts may propeller themselves by decreasing the temperature.
Remark 2. In reality, heated air is lighter and moves upwards due to buoyancy. This will be further discussed in Section 5, below.
8.4. Horizontal solutions on a plane boundary surface, e.g. leaves or a shield
Consider a shield a distance from a source. With the velocity u proportional to a coordinate y from the center and parallel with the matter, H=H(y) in (3) gives
(H'(y)rL +Cu)dy=-drL H (3)
where C is a constant. Next, we will tacitly include time to obtain a semi-analytical solution. With drL having support at the layer; drL~dy and H initially being the Dirac delta distribution at a coordinate, a Heavyside function is obtained for the temperature, H. This is a promising solution for heat to spread sideways on a wide shield. With the symmetric solution H~u2 , derived in Section 3, the entire shield will be heated. However it may extend (violate), the preliminaries for the scale of a material point in a Lagrangian frame with local coordinates. More realistic solutions may be arrived with approximations:
H'(y)rL <<Cu and drL proportional to dy, gives H(y) proportional to Cu
H'(y)rL>>Cu and drL prop. to dy, gives H'(y) proportional to H, i.e. exponential solutions.
8.5. Spatial Buoyancy model with Pressure domination
Heated air gets lighter and moves upwards due to buoyancy. These boundary actions with relative motions are not included in the pointwise BL (1), however the pressure function may rule and balance into such streaming expressions. The upward velocity for the light hot air may increase and decrease with a distance y, c.f. Figure 5.
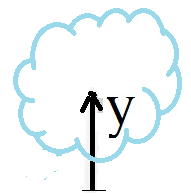
Figure 5. Vertical coordinate y, for a parcel of hot air moving upwards due to buoyancy.
With a balance for kinetic energy and pressure, this will be proposed with functional relations:
Density is decreasing when lighter air with higher temperature upwards. A pressure potential for this uplift
is proposed to read; p(y)= -Pym exp(-sy) …… (4
where P,m and s are parameters and y is a vertical coordinate, Figure 3.
With d=1, the velocity from an energy balance similar to (1); du2/2+p=C, is given by
u=2sqrt(C+Pymexp(-sy)) …. (5)
For some values of the parameters (C,m,s), u=u(y) is shown in Figure 6, with the code Maxima Online
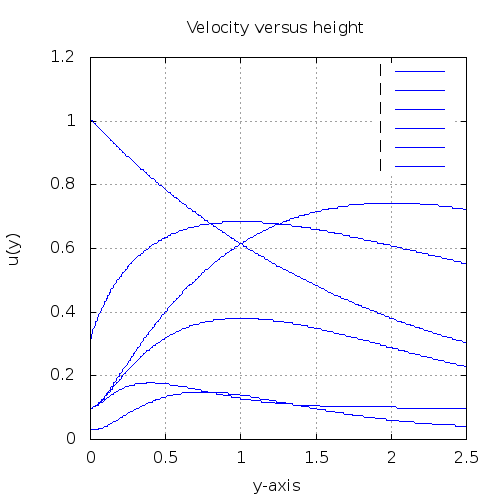
Figure 6. Draw2d( /* global options */ title = “Velocity versus height”, xlabel = “y-axis”, ylabel = “u(y)”, grid = true, dimensions = [500,500], /* implicit function */ key = “I”,
implicit(sqrt(0.01+exp(-x))-y , x, 0,2.5, y, 0,1.2), implicit(sqrt(0.1+x*exp(-x))-y , x, 0,2.5, y, 0,1.2),
implicit(sqrt(0.01+x*x*exp(-x))-y , x, 0,2.5, y, 0,1.2), implicit(sqrt(0.01+x*x*exp(-2*x))-y , x, 0,2.5, y, 0,1.2)
, implicit(sqrt(0.01+x*x*exp(-5*x))-y , x, 0,2.5, y, 0,1.2)) , implicit(sqrt(0.001+x*x*x*exp(-4*x))-y , x, 0,2.5, y, 0,1.2);
8.5.1. ntinuum fluid analysis
The pressure function (4), is a constitutive equation dependent on an inverted length-scales and a non- dimensional parameter m. Since approaching zero at boundaries, it may serve to model pressure both vertically (at the buoyancy) and horisontally.
A differentiation of p(y) or, for brevity, ln(p/P), gives maximum at y=m/s.
A known distribution related to temperature is the pressure of an acoustic medium. For an array of hot candle spots, it is found to give a significant heat wave in reflecting semi-thick steel plates. Maybe also with only one hot spot, a more efficient surrounding shield can be created with a certain geometry. Another possibility is to use a galvanic stress into a spreading on a material.
Remark. The pressure function proposed in (4) in a periodic [] pattern may trigger acoustic behaviour, which at occasions (subjected to small perturbations, or due to rules for sound waves being dual) appears in other distributions, thus giving inputs to heat.
8.5.2 Derivation into functional formats
In continuum mechanics, the constitutive equations do not include coordinates. With the assumptions proposed above, a relation without coordinates for specific mechanical power will be derived.
Subsequently this will be referred to as specific power or power.
Theorem 1. Neglecting the constant C in the velocity u ; equation (5), the (mechanical power)/(unit volume) p*u,y for a material point reads …… ½ sqrt(p) p'(y) ….. (6)
Proof: Differentiation of (5) and (4) and substitution of p from (4), assuming C=0.
This specific power enters in a balance with rate of energy. Energy E, is assumed proportional to temperature as E=dcH where c is a specific heat parameter.
Remark. Geometrically, p may be naturally composed such that the sqrt gives a format of coordinates with ‘integer-degree’ ; i.e. xk, where k is an integer, which means an area measure or composition of such.
8.5.3. Decomposition into energy balance
Example. Consider a horisontal sequence of p(y) from (4), on lengths of magnitude 2m/s, i.e. the pressure function repeated periodically. This constitutes the spatial pattern of a stationary wave. Insertion of the expression p'(y)=p(y)(m/y-s) in (6) gives two parts. The first part is more concentrated close to y=0, and the other part is the function ½(-s)p(3/2), i.e. similar to the pressure p(y), but with other parameters.
In order to describe temperature, we will compare with the balance equation for energy E, in continuum mechanics, when neglecting heat flux
E,t + u*grad(E) =pu,y …………….. (9)
Remark. Neglecting heat flux is motivated when pressure dominates, and describes more rapid and local behaviour. Heat conduction by diffusion can occur afterwards and in surrounding areas.
Next, we will discuss how the two terms at the left side of (9), could be balanced by each term in (6): With E=dcH, as suggested in section 5.2, the time differential of E may be negative when the temperature rises and the density decreases. That is known to happen generally for heated fluids (and is known as buoyancy [3,4]) Hereby, the first term may balance the negative term, (-s)p(3/2)/2, at the right side.
The other term ½(m/y)p(3/2)/2 is more concentrated and may have a singularity. That could be a distribution for the light (‘one hot spot’), and the gradient of E may still spread in other directions than the velocity. In general, the direction of the velocity could also be horisontal and then generate a temperature gradient along a shield. (A sub-structure localised velocity may emanate from local buoyancy or be a particle velocity in a stationary sound -wave.)
8.5.4. Singularity for specific power (6), in terms of bound for m
For smaller values of the parameter m than in Figure 4, the distribution for specific power can be singular.
Preliminaries. A singularity at y=0 is defined as yk where k<0.
Exercise. Derive the bound for m at which the first term in (6) has a singularity.
Solution. Insertion of (4) and p'(y) in (6) gives the exponent for y ; reading 3m/2-1 … (10). From the preliminaries 3m/2-1<0 , i.e. m<2/3.
In Figure 7, the pressure p(y) from (4) is shown for m=0.5 and s=0.9, 0.5. The strength of the singularity
for specific power (6) is given by (10), i.e. 3/4-1=-1/4.
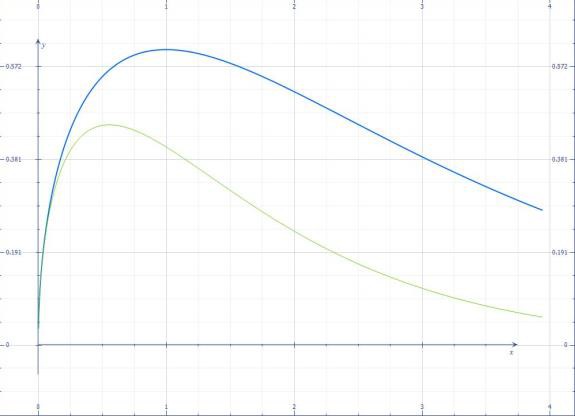
Figure 7. Pressure function (4), p(y)/-P= ym exp(-s*y) with parameter m<2/3, such that the power (6) is singular at origin. Upper curve m=0.5, s=0.5. Lower curve m=0.5, s=0.9.
Remark. Consider equation (9), when heat conduction is included and (grad E) is perpendicular to u such that convection vanishes. When the singular part of power balances the Laplacian of temperature, a Poisson’s equation similar to that of gravity for a ‘density’-distribution, is obtained.
Exercise. For m<0, i.e. when the entire pressure is singular at the boundary y=0, a stronger singularity is obtained for the specific power; expression (6). Derive the exact expression.
8. Methods for realisation of Energy equivalents
Next, realisations of the results will be outlined, in terms of devices and configurations:
Light equivalent. A spherical bulb next to the growth, reflecting low intense light c.f. Figure 1, gives several opportunities, e.g. more light, a mirror and a larger geometry to copy, [1].
Other light equivalent may be given by oscillations from high-frequency sound. This also provides a pressure.Heat equivalent. Heat may be provided by sound given by an acoustic pressure [2]. This is easily arranged with not so high electricity input. Also a mechanical clockwork could possibly be used. Temperature is given by pressure, according to constitutive equations in thermostatics. Equivalent acoustics could be provided in the plant (when considered as a battery with a galvanic stress), and generated by its own howl,
i.e. audio feedback, given by an integrated microphone in a loudspeaker consisting of plastic or aluminum[22].
Temperature gradient. Next to a wall, might be a place to survive at winter. There, the plant may use the temperature gradient as an energy provider to produce heat. This can be cast into formula language within Thermodynamics [26, 27] and Legendre transformations.
The Legendre Transformation formula is given as: g ( p ) = sup x { p x − f ( x ) } , where f ( x ) is the original function, x its variable, p the derivative of f with respect to x , and g ( p ) the Legendre transformed function.
Theorem. From the definition, an energy function E is given by the Legendre transformation E=px-f(x).
When the original function f(x) is a pressure proportional to temperature at a point x, T(x), the new function reads E=grad T*x- f(x)
Proof. From the chain rule for derivatives p=f,x=f,T T,x where ,x denotes partial x-derivative.
Partial shade. A dynamic pattern of partial shade mimics when matter grows into leaves. For some species, possibly an artificial creation with alternating light, may be beneficial.
9. Conclusion
Energy equivalent measures for e.g.
- a spherical bulb
- acoustic pressure
- temperature and temperature gradients
were given and exemplified with growth and cultivation of plants. Transformation into green bulk or energy were cast into formulas with angular velocities, field theories and Thermodynamics. Some types of growth was identified as the material in an aura given by the path of a nco. A future issue is to use magnets [1,s29, s30] and evaluate benefits in e.g. a cold climate. Additional features are to analyse the copying and adjacency to bio-matter [31], to obtain energy and perceptance into a format suitable for e.g. winter-rest. The Classical Black Hole characterisation in conjunction with wave dynamics [32] is also a topic with possibilities, e.g. if acoustic feed-back may replace light energy to some extent.
10. Acknowledgements. To the J-T lab, making it possible to do the in-situ observations and in-vivo experiments. To the reference of Chaffin (Wave-Flow Interactions and Acoustic Streaming, (2016) pp 10), about aspects of continuum mechanics with applications.
11.References.
[1] Strömberg L J-T. (2021). Battery Pot Plants with Magnets and Adjacent Balloon as Substitutes for Light. Journal of Human Earth and Future 2(2):136-139
[2]Halder, A., Tanshen, M. R., Hossain, M. A. ., Akter, M. S. ., & Sikdar, M. A. . (2023). Tailored Dispersion and Nonlinear Effects in Flint Glass Honeycomb PCF for Optical Communication. Journal of Optics and Photonics Research, 1(1), 43-49.
[3] Soualmia, Adel & Chenni, Rachid. (2018). Performance analyses of grid-connected photovoltaic power system. Journal of Renewable Energies. 21. 623-634. 10.54966/jreen.v21i4.716.
Soualmia, Adel & Chenni, Rachid. (2016). Soualmia A , Chenni R (2016). Modeling and Simulation of
Photovoltaic Production Losses due to Partial Shade. Poster Setit, Springer IEEE.
[4] Pellis, Stergios. (2024). The Formulas of the Dimensionless Universe. SSRN Electronic Journal. 3. 63. 10.2139/ssrn.4792077.
[5] Anderson, Douglas & Onitsuka, Masakazu. (2025). Ulam Stability and Instability of First-Order Linear
$$\omega $$ -Periodic Dynamic Equations on Isolated Time Scales. 10.1007/978-3-031-83327-4_2.
[6] Osman, Mahmoud & Saker, Samir & Anderson, Douglas. (2025). On Some Pachpatte-Type Dynamic Inequalities and Their Applications. Qualitative Theory of Dynamical Systems. 24. 10.1007/s12346-025- 01287-x.
[7] Strömberg L (2023). Response to curvature, gradients and temperature in a PPB-fuel cell, with a LED and a Li-B. Advances in Environment and Energies, Sanderman PH. Volume 2, Issue 1, No. 3.
[8] Robertson, Glen. (2023). VEM Drive as a Buoyancy Effect. 10.13140/RG.2.2.13814.98886.
[9] Li, Scott & Woods, Andrew. (2023). Boundary mixing. Part 1. Transport of buoyancy and passive tracer. Journal of Fluid Mechanics. 976. 10.1017/jfm.2023.796.
[10] Omar, Ihab & Saleh, Ahmed & Alhusseny, Ahmed. (2024). Theoretical and experimental investigation of the effect of heat flux to lift water in a solar bubble pump. Engineering and Technology Journal. 1-10. 10.30684/etj.2024.145911.1669.
[11] Ali Benhmidene, Rabeb Jemaii, Khaoula Hidouri, Bechir Chaouachi (2022) Study of flow fluctuation in the thermal bubble pump tube By IJTFEDITOR
Volume 9, Issue 3, Paper No. 090305
[12] Manconi, Elisabetta & Sorokin, Sergey & Garziera, Rinaldo & Søe-Knudsen, Alf. (2018). Wave Motion and Stop-Bands in Pipes with Helical Characteristics Using Wave Finite Element Analysis. Journal of Applied and Computational Mechanics. 4. 420-428. 10.22055/JACM.2018.24930.1218.
[13] https://doc.freefem.org/tutorials/thermalConduction.html https://doc.freefem.org/tutorials/poisson.html
[14] Brzenski, Jared & Castillo, Jose. (2023). Solving Navier-Stokes with Mimetic Operators. Computers & Fluids. 10.1016/j.compfluid.2023.105817.
[15] Riesen P, Hutter K, Funk M (2010). A viscoelastic Rivlin-Ericksen material model applicable to glacier ice, Nonlin. ProcessesGeophys., 17, 673–684, https://doi.org/10.5194/npg-17-673-2010
[16] Crane, Keenan & Weischedel, Clarisse & Wardetzky, Max. (2013). Geodesics in Heat: A New Approach to Computing Distance Based on Heat Flow. ACM Transactions on Graphics. 32. 10.1145/2516971.2516977.
[17] Liu, Wing & Li, Shaofan & Park, Harold. (2022). Eighty Years of the Finite Element Method: Birth, Evolution, and Future. Archives of Computational Methods in Engineering. 29. 10.1007/s11831-022- 09740-9.
[20] Sorokin, S.V. (2004). Analysis of wave propagation in sandwich plates with and without heavy fluid loading. Journal of Sound and Vibration – J SOUND VIB. 271. 1039-1062. 10.1016/j.jsv.2003.03.003.
[22] J-T Strömberg , L., & Benhmidene , A. (2022). Evaluation of Coil-Induction, Foil-Capacity and Growth in Pot Plant Batteries. Asian Journal of Research and Reviews in Physics, 6(4), 32–38. https://doi.org/10.9734/ajr2p/2022/v6i4127
[26] Truesdell, Clifford & Noll, Walter (2004). The Non-Linear Field Theories of Mechanics. Springer. ISBN 978-3-662-10388-3.
[27] Meyn, Jan-Peter. (2024). A Contemporary View on Carnot’s Réflexions. Entropy. 26. 1002. 10.3390/e26121002.
[29] Herman, H., Kaniawati, I., Setiawan, A. And Rusdiana, D., The Use Of Magnetometer Sensors In Physics Experiments: The Motion Of Objects With Constant Velocity And Constant Acceleration.
[30] Dorfmann L, Ogden RW. 2023 The nonlinear theory of magneto elasticity and the role of the Maxwell stress: ar eview. Proc. R. Soc. A479: 20230592.https://doi.org /10.1098/rspa.2023.0592
[31] Benvenuti, Elena & Reho, Gino & Palumbo, Stefania & Fraldi, Massimiliano. (2022). Pre-Strains and Buckling in Mechanosensitivity of Contractile Cells and Focal Adhesions:A Tensegrity Device. SSRN Electronic Journal. 10.2139/ssrn.4142057.
[32] Kvist, Kristian & Sorokin, Sergey. (2024). Asymptotic analysis of acoustic black hole effect in cylindrical shells. The Journal of the Acoustical Society of America. 155. 3426-3435. 10.1121/10.0026083.
