Investigating Diatomic Homonuclear Molecules

Introduction: Molecules are a collection of two or more atoms held together by a chemical bond. Molecules may be homonuclear, contain atoms of one chemical element, such as two atoms in the oxygen molecule, or they may be heteronuclear, consisting of more than one chemical element, such as a molecule of water since it has two different atoms. A covalent bond is a chemical bond that contains the sharing of electron pairs between atoms.

A chemical bond is a collection of atoms or ions that constitute molecules and crystals. The chemical bond may be attributed to the electric force between charged ions with opposite signs, as in ionic bonds, or by the sharing of electrons, as in covalent bonds. The polarity, directionality and the strength of bonds can be determined through octet rule, theory of Valence Shell Electron Pair Repulsion (VSEPR), and the theory of Valence Bond (VB), which contains orbital hybridization, resonance and molecular orbital theory, which comprises a linear combination of ligand field theory and atomic orbitals [1- 6].

Covalent radius is the smallest distance between two atoms bonded together with sharing of electrons. It is the distance between two atoms approaching each other without interfering. The sum of the two covalent radii is equal to the covalent bond length between two atoms. The bond lengths are measured by neutron diffraction on molecular crystals or X-ray diffraction. Rotational spectroscopy gives precise values of bond lengths [7 – 10].

Small systems such as atoms and molecules have constant values because of the homogenous distribution of their constituents. It is found that the atom as a nucleus and electrons at certain distances are contained in a certain area with a certain uniform distribution forming a certain system (atom) with a certain constant (1.1 X 10⁸ m²/Kg) [11]. The same result with certain constant (5.4 X 10⁹ m^-1) is found for homonuclear molecules as a sharing of electron pairs between two similar atoms with uniform distribution to form certain covalent chemical bonds.

Materials and Methods

Physical relations and laws can be expressed regarding the main physical parameters responsible for their origin. The shared electrons between two atoms forms a covalent bond with a certain uniform distribution, producing a certain uniform system (molecule).

The main goal of collective covalent radii is to estimate approximately as given in equation (1), the length of a bond as the sum of two atomic radii

The origin for these covalent radii for single bonds is found in [12]. The list of metallic bonding and VCH periodic table is reported in [13,14]. In simple terms, a single bond corresponds to an electron pair in a bonding molecular orbital.

The covalent radii in pure-bred shape are determined by bisecting a homonuclear bond, as shown in the following equation (2).

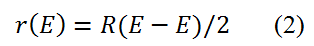
The new group of single bond covalent radii for the elements 1 – 96, based on enormous data mining from the Cambridge Structural Data Base (CSD) and estimating the carbon radii (separately for the three familiar hybridizations), nitrogen and oxygen is found in [15].

The present scheme and method to determine the covalent radii are different. We considered diatomic homonuclear molecules as equal in their spherical geometrical shape. All covalent radii are then obtained self-consistently by using a simple equation connecting the radius, which represents the covalent radius and several sharing electrons. Our approach confirms that the diatomic homonuclear molecules have spherical shape and its mathematical relation can be used to calculate covalent radii and confirm certain constant (5.4 X 10⁹ m^-1)

Results and Discussions

Density Functional Theory (DFT) is a powerful method utilized in both physics and chemistry to investigate the electronic structure (especially the ground state) for atoms and molecules. Using this theory, the characteristics of a many-electron arrangement can be estimated. In spite of late improvements, there are some difficulties in using DFT to describe intermolecular interactions such as realizing chemical reactions, particularly van der Waals forces [16-17].

Molecular Orbital (MO) theory provides a method to describe the electronic structure of molecules by using molecular quantum mechanics or quantum chemistry. MO theory treating the states of bonded electrons – the molecular orbitals – as Linear Combination of Atomic Orbitals (LCAO) by using the models of Density Functional Theory (DFT) to the Schrodinger equation. These are represented by three kinds (bonding, antibonding, non – bonding). A bonding orbital intensifies electron density in the area between a particular couple of atoms, consequently its electron density will tend to pull each of the two nuclei toward the other and hold the two atoms together [18 – 19].

The participation of electrons between two atoms to form covalent bonds leads to the formation of particular molecules. Diatomic homonuclear molecules are formed with certain geometrical shape (spherical) with a certain circumference for each molecule. It is found that the covalent radii of this type of molecules behave linearly as a result of increasing atomic number in periodic table. The model is based on the number of sharing electrons and the circumference and both of them are increasing with increasing atomic number.

 It is found that the proportionality between cubic root of the number of shared electrons and circumference for diatomic homonuclear molecules gives the accurate results with experimental values equations as shown in equations (3 & 4 & 5)

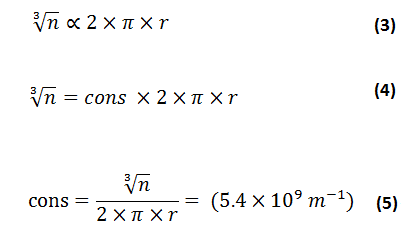
From which the following equation can be deduced

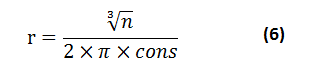
The calculated covalent radius of homonuclear molecules by using equation (6) is consistent and in good agreement with experimentally determined radii values [20] as indicated in Table 1

where

n is the number of electrons of two atoms

r is the covalent radius

cons. is constant value for molecules

All calculations confirmed that there is a constant value (5.4 X 10⁹ m^-1) for molecules formed by covalent bonds relating to the cubic root of the number of electrons and their circumference. Table (1) lists the constant value of similar molecules consisting of one chemical element by using equation (5).  

A comparison of the present calculations and results for the covalent radius of diatomic homonuclear molecules with the available experimental values shows a good agreement between them [8].

The physical meaning of the constant of diatomic homonuclear molecules represents the number of sharing electrons to form certain covalent bond and radius of spherical geometrical shape of this type of molecules.   

There are only seven calculated covalent radii approximately 5 % from 118 molecules by using equation (3) are deviated from the experimental determined values for the elements (Lithium, Beryllium, Sodium, Magnesium, Aluminium, Silicon, Phosphorus). The difference may be referred to the deviation of these molecules from spherical geometrical shape. 

Table 1. List the experimental and new covalent radii.

Atomic Number	Symbol	Name	Experimental Covalent Radius picometer (pm)	New Covalent Radius picometer (pm)	Constant
1	H	Hydrogen	32	37	5.4 X 109
2	He	Helium	46	47	5.4 X 109
3	Li	Lithium	133	54	5.4 X 109
4	Be	Beryllium	102	59	5.4 X 109
5	B	Boron	85	63	5.4 X 109
6	C	Carbon	75	67	5.4 X 109
7	N	Nitrogen	71	71	5.4 X 109
8	O	Oxygen	63	74	5.4 X 109
9	F	Fluorine	64	77	5.4 X 109
10	Ne	Neon	67	80	5.4 X 109
11	Na	Sodium	155	82	5.4 X 109
12	Mg	Magnesium	139	85	5.4 X 109
13	Al	Aluminium	126	87	5.4 X 109
14	Si	Silicon	116	90	5.4 X 109
15	P	Phosphorus	111	92	5.4 X 109
16	S	Sulfur	103	94	5.4 X 109
17	Cl	Chlorine	99	96	5.4 X 109
18	Ar	Argon	96	98	5.4 X 109
19	K	Potassium	196	99	5.4 X 109
20	Ca	Calcium	171	101	5.4 X 109
21	Sc	Scandium	148	103	5.4 X 109
22	Ti	Titanium	136	104	5.4 X 109
23	V	Vanadium	134	105	5.4 X 109
24	Cr	Chromium	122	106	5.4 X 109
25	Mn	Manganese	119	108	5.4 X 109
26	Fe	Iron	116	110	5.4 X 109
27	Co	Cobalt	111	111	5.4 X 109
28	Ni	Nickel	110	112	5.4 X 109
29	Cu	Copper	112	114	5.4 X 109
30	Zn	Zinc	118	115	5.4 X 109
31	Ga	Gallium	124	116	5.4 X 109
32	Ge	Germanium	121	117	5.4 X 109
33	As	Arsenic	121	118	5.4 X 109
34	Se	Selenium	116	119	5.4 X 109
35	Br	Bromine	114	121	5.4 X 109
36	Kr	Krypton	117	122	5.4 X 109
37	Rb	Rubidium	210	123	5.4 X 109
38	Sr	Strontium	185	125	5.4 X 109
39	Y	Yttrium	163	126	5.4 X 109
40	Zr	Zirconium	154	127	5.4 X 109
41	Nb	Niobium	147	128	5.4 X 109
42	Mo	Molybdenum	138	129	5.4 X 109
43	Tc	Technetium	128	130	5.4 X 109
44	Ru	Ruthenium	125	131	5.4 X 109
45	Rh	Rhodium	125	132	5.4 X 109
46	Pd	Palladium	120	132	5.4 X 109
47	Ag	Silver	128	133	5.4 X 109
48	Cd	Cadmium	136	134	5.4 X 109
49	In	Indium	142	135	5.4 X 109
50	Sn	Tin	140	136	5.4 X 109
51	Sb	Antimony	140	137	5.4 X 109
52	Te	Tellurium	136	138	5.4 X 109
53	I	Iodine	133	139	5.4 X 109
54	Xe	Xenon	131	140	5.4 X 109
55	Cs	Cesium	232	141	5.4 X 109
56	Ba	Barium	196	142	5.4 X 109
57	La	Lanthanum	180	143	5.4 X 109
58	Ce	Cerium	163	144	5.4 X 109
59	Pr	Praseodymium	176	144	5.4 X 109
60	Nd	Neodymium	174	145	5.4 X 109
61	Pm	Promethium	173	145	5.4 X 109
62	Sm	Samarium	172	146	5.4 X 109
63	Eu	Europium	168	147	5.4 X 109
64	Gd	Gadolinium	169	148	5.4 X 109
65	Tb	Terbium	168	149	5.4 X 109
66	Dy	Dysprosium	167	149	5.4 X 109
67	Ho	Holmium	166	150	5.4 X 109
68	Er	Erbium	165	150	5.4 X 109
69	Tm	Thulium	164	151	5.4 X 109
70	Yb	Ytterbium	170	152	5.4 X 109
71	Lu	Lutetium	162	153	5.4 X 109
72	Hf	Hafnium	152	153	5.4 X 109
73	Ta	Tantalum	146	154	5.4 X 109
74	W	Tungsten	137	155	5.4 X 109
75	Re	Rhenium	131	156	5.4 X 109
76	Os	Osmium	129	156	5.4 X 109
77	Ir	Iridium	122	157	5.4 X 109
78	Pt	Platinum	123	157	5.4 X 109
79	Au	Gold	124	158	5.4 X 109
80	Hg	Mercury	133	159	5.4 X 109
81	Tl	Thallium	144	159	5.4 X 109
82	Pb	Lead	144	160	5.4 X 109
83	Bi	Bismuth	151	161	5.4 X 109
84	Po	Polonium	145	161	5.4 X 109
85	At	Astatine	147	162	5.4 X 109
86	Rn	Radon	142	162	5.4 X 109
87	Fr	Francium		163	5.4 X 109
88	Ra	Radium	201	164	5.4 X 109
89	Ac	Actinium	186	165	5.4 X 109
90	Th	Thorium	175	165	5.4 X 109
91	Pa	Protactinium	169	166	5.4 X 109
92	U	Uranium	170	167	5.4 X 109
93	Np	Neptunium	171	168	5.4 X 109
94	Pu	Plutonium	172	169	5.4 X 109
95	Am	Americium	166	170	5.4 X 109
96	Cm	Curium	166	170	5.4 X 109
97	Bk	Berkelium	168	170	5.4 X 109
98	Cf	Californium	168	171	5.4 X 109
99	Es	Einsteinium	165	171	5.4 X 109
100	Fm	Fermium	167	171	5.4 X 109
101	Md	Mendelevium	173	172	5.4 X 109
102	No	Nobelium	176	172	5.4 X 109
103	Lr	Lawrencium	161	173	5.4 X 109
104	Rf	Rutherfordium	157	173	5.4 X 109
105	Db	Dubnium	149	175	5.4 X 109
106	Sg	Seaborgium	143	175	5.4 X 109
107	Bh	Bohrium	141	176	5.4 X 109
108	Hs	Hassium	134	176	5.4 X 109
109	Mt	Meitnerium	129	176	5.4 X 109
110	Ds	Darmstadtium	128	176	5.4 X 109
111	Rg	Roentgenium	121	177	5.4 X 109
112	Cn	Copernicium	122	178	5.4 X 109
113	Nh	Nihonium	136	179	5.4 X 109
114	Fi	Flerovium	143	179	5.4 X 109
115	Mc	Moscovium	162	180	5.4 X 109
116	Lv	Livermorium	175	180	5.4 X 109
117	Ts	Tennessine	165	181	5.4 X 109
118	Og	Oganesson	157	181	5.4 X 109

It is noticed that all homonuclear molecules have the same value (5.4 X 10⁹ m^-1) This means and indicates that all molecules have the same constant value relating to the cubic root of the number of electrons and their circumference.

Conclusion

The homogenous distribution of participating or sharing electrons for diatomic homonuclear molecules formed by covalent bonds with a certain number and certain circumference leads to the existence of a common constant for all diatomic homonuclear molecules. The cubic root of the number of sharing electrons and their circumference gives constant value with calculations and results of covalent radii in good agreement with experimental determinations.

Acknowledgement

“The author would like to express his sincere appreciation and deepest gratitude to the anonymous referee and all the staff of the United Journal of Chemistry whose contribution and support have greatly enhanced the quality, accuracy and publication of this research”

Conflict of interest

The author declares no conflicts of interest.

References

1. Levine, D. S.; Martin, H. G. Clarifying the quantum mechanical origin of the covalent chemical bond. Nature Communications. 2020, 11, 4893
2. Allen, F. H.; Kennard, O.; Watson, D. G.; Brammer, L.; Orpen, A.G.; Tylor, R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds. J. Chem. Soc., Perkin Trans. 1987, 2 (12), S1-S19.
3. Frenking, G.; Krapp, A. Unicorns in the world of chemical bonding models. Journal of   Computational Chemistry. 2007, 28 (1), 15–24.
4. Gillespie, R. Teaching Molecular Geometry with the VSEPR Model. Journal of Chemical Education. 2004, 81 (3), 298-304
5. Harwood, W.S.; Herring. F.G, General Chemistry: Principles and Modern Applications (8th ed.). 2002, Prentice-Hall. ISBN 978-0-13-014329-7. 
6. Bader, R. F. W.; Gillespie, R. J.; MacDougall, P. J. A physical basis for the VSEPR model of molecular geometry. J. Am. Chem. Soc. 1988, 110 (22): 7329–7336.
7. Hund, F. Zur Deutung der Molekelspektren. IV. Zeitschrift für Physik. 1928, 51 (11–12), 759 – 795.
8. Orpen, A. G.; Brammer, L.; Frank, H. A.; Olga, K.; Watson, D. G.; Tylor, R. Tables of bond lengths determined by X-ray and neutron diffraction. Part 2. Organometallic compounds and co-ordination complexes of the d- and f-block metals. Journal of the Chemical Society, Dalton Transactions. 1989, S1-S83.
9. Sanderson, R. T. Electronegativity and bond energy. Journal of the American Chemical Society. 1983, 105 (8), 2259-2261.
10. Pauling, L. The Nature of the Chemical Bond. II. The One-Electron Bond and the Three Electron Bond. Journal of the American Chemical Society. 1931, 53 (4), 3225-3237.
11. Sanad, M. R. Constant of Atoms and New Equation of Electromagnetic Force. Proceedings of the Romanian Academy, series A. 2024, 25 (4), 301-306.
12. Pauling, L. The Nature of the Chemical Bond, 3rd ed., Cornell University Press, Ithaca, NY, 1960.
13. Pauling, L; Kamb, B. Proc. Natl. Acad. Sci. USA, 1986, 83, 3569 – 3571.
14. Fluck, E; Heumann, K.G. Periodensystem der Elemente, 3rd ed., Wiley-VCH, Weinheim, 2002.
15. Cordero, B.; Gómez, V.; Platero-Prats, A, E.; Revés, M.; Echeverría, J.; Cremades, E.;  Barragán, F.; Alvarez, S. Covalent radii revisited. Dalton Trans. 2008, 2832-2838.
16. Assadi, M. H. N.; et al. “Theoretical study on copper’s energetics and magnetism in TiO₂ polymorphs”. Journal of Applied Physics. 2013, 113 (23): 233913–233913–5
17. Medvedev, Michael G.; Bushmarinov, Ivan S.; Sun, Jianwei; Perdew, John P.; Lyssenko, Konstantin, “Density functional theory is straying from the path toward the exact functional”. Science. 2017, 355 (6320): 49–52
18. Miessler and Tarr, Inorganic Chemistry, 2013, 5th ed, 117-165, 475-534
19. Albright, T. A.; Burdett, J. K.; Whangbo, M.-H. Orbital Interactions in Chemistry. 2013, Hoboken, N.J.: Wiley.
20. Pyykkö, P.; Atsumi, M. Molecular Single-Bond Covalent Radii for Elements 1–118.  Chemistry: A European Journal. 2009, 15 (1), 186-197.