Introduction
Because of their extraordinary properties, single-walled nanotubes (SWNTs) can be considered as attractive candidates in diverse nanotechnological applications, such as molecular devices, molecular tanks, (bio) sensors, drug delivery, and many others [1-12]. It has been demonstrated that SWNTs can interact with different classes of compounds, and the formation of supramolecular complexes allows a better processing of SWNTs toward the fabrication of innovative nanodevices [13-16]. Among the many well-known exohedral reactions developed on
the SWNTs, heterocycle rings construct interesting combinations with these all sp2-carbons ring systems [17-23]. For example, fusion with six-membered heterocycles was extended on the basis of the hetero-Diels-Alder reaction [24], and fusion with five-membered heterocyclic rings was performed by using various 1,3-dipolar cycloaddition reactions [25, 26]. A considerable part of these studies dealt with the [2+1] cycloaddition of carbenes to nanostructures, such as carbon nanotubes and fullerenes. The [2+1] cycloadditions of carbenes to pristine carbon nanotubes were first employed by the Haddon group [27-29]. It was found that such covalent modification result in the formation of derivatized SWCNTs, soluble in dimethyl sulfoxide or 1,2- dichlorobenzene. The [2+1] cycloaddition reactions exert stronger effects on the electronic band structures of metallic SWNTs [16, 29].
Within the different classes of nanotubes made of carbon or noncarbon materials which exhibit interesting electronic, mechanical, and structural properties, ternary boron carbonitride nanotubes (BCN-NTs) are extremely promising for applications in nanotechnology. Some of Cx(BN)y nanotubes, such as BCxN (1<x<5) ones, have been successfully synthesized by using different experimental methods [30-36]. Among BCN nanostructures, BC2N is believed to be one of the most stable stoichiometries [37], which was first reported in 1995 by Weng-Sieh et al. [33].
Azevedo [38] showed that the electronic structures of the BC2N nanotubes strongly depend on the pattern and the composition of C and BN within the tube lattice. There can be more than one type of zigzag or armchair BC2N-NTs, depending on how a BC2N sheet is rolled up [39]. In two types of zigzag BC2N nanotubes, C-C units are isolated, leading to preactivated sites for preferential exohedral reactions such as regioselective multiadditions [40-42]. This offers a significant opportunity for the creation of new nanostructures with potential applications in biological and materials science. During the last 15 years, chemists have uncovered several inherent regioselectivity principles in multiadditions ,and have also developed new concepts such as tethering and templating strategies for controlled multiple additions. The degree and pattern of addition determine the electronic and chemical properties of the functionalized fullerenes and SWNTs.
So it can be a good idea to investigate, in the present work, the multiple [2+1] cycloaddition of carbenes to the isolated C=C bonds in the (n, 0) BC2N nanotubes with n= 4, 5, and 6 in terms of geometry, energy, stability, electronic structure, and natural bonding orbital (NBO) analysis. Three carbenes with different neutral chemical groups, namely (1) CH2, (2) CF2, and (3) CHF, are introduced as the substituents of the BC2N nanotubes to address these questions: are BC2N- NTs favorable for [2+1] cycloadditions? How does the [2+1] cycloaddition affect the electronic properties of BC2N-NTs? Are BC2N-NTs more or less reactive toward [2+1] cycloaddition than their carbon analogues? It must be noted that the main purpose of this study is focused on the effect of the hydrogen bondings on the stability of the considered functionalized BC2N nanotubes. We attempt to characterize the geometry and strength of intramolecular hydrogen bondings by means of natural bonding orbitals (NBO) analysis in terms of delocalization (or charge transferring) effects [34]. Our results may be useful for further studies in functionalization of the BC2N nanotubes and construction of nanodevices.
![Fig. 1- Optimized structures of pristine ZZ-3 (4, 0) BC2N nanotube and the complex of ZZ-3 (4, 0)/(CH2)6 as an [2+1] cycloaddition product.](http://unitedjchem.org/wp-content/uploads/2018/08/03-1-150x150.jpg) |
|
Computational Aspects
Adopting the same notations as those in Ref. 29, we consider ZZ-3 (n, 0) zigzag BC2N single- walled nanotubes with n=3, 4, and 5, see Fig.1. These systems all have approximately 100-160 atoms, and the dangling bonds at the ends are tied off with hydrogen atoms. Osuna et al. [19] have indicated that inclusion of dispersion corrections is compulsory for the study of the chemical reactivity of fullerenes and nanotubes. They performed calculations both with and without dispersion corrections for the Diels−Alder reaction of (5, 5) single-walled carbon nanotube with several dienes, and showed that these corrections are essential to get results close to the experimental values. Therefore, we carry out ab initio calculations by using the M06-2X functional. The M06-2X functional belongs to a new generation of hybrid meta-generalized- gradient-approximation exchange–correlation functionals which include an accurate treatment of the dispersion energy. The M06-2X functional [43] in combination with 6-311G(d, p) basis sets are used for geometry optimizations and single-point energy calculations. The standard 6- 311G(d, p) basis set is employed due to being affordable and accurate enough for geometry optimization of even large molecules [44, 45].The optimized structures of the complexes of three carbenes (CH2), difluorocarbene (CF2) and (CHF) with ZZ-3 (n, 0) BC2N nanotubes, i.e. (n, 0)/(CH2)n, (n, 0)/(CH2)2n, (n, 0)/(CF2)n, (n, 0)/( CF2)2n, (n, 0)/(CHF)n, and (n, 0)/(CHF)2n, with n=3, 4, and 5, are shown in Fig. 2. Frequency calculations are carried out for all of the systems at the same level of theory, and real obtained frequencies confirm that all of them are structures with the minimum energy. All DFT calculations have been performed using GAMESS suite of programs [46].
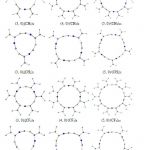 |
Table 1. Total energies (Et in a.u.), HOMO energy (EHOMO), LUMO energy (ELUMO), HOMO- LUMO energy gaps (Eg), and reaction energy (Er) in eV, and geometrical parameters in Å for [2+1] cycloaddition products of the BC2N nanotubes with carbenes.
| Et | EHOMO | ELUMO | Eg | Er | C1-C2 | C2-C3 | |
| (3, 0) (CH2)6 | -3047.06 | -4.68 | -2.64 | 2.04 | -1.55 | 1.533 | 1.538 |
| (3, 0)/(CH2)3 | -2929.27 | -4.63 | -3.00 | 1.63 | 1.17 | 1.521 | 1.531 |
| (3, 0)/(CF2)6 | -4237.47 | -5.32 | -3.15 | 2.17 | 1.23 | 1.564 | 1.511 |
| (3, 0) /(CF2)3 | -3524.54 | -5.00 | -3.35 | 1.65 | 3.42 | 1.550 | 1.495 |
| (3, )/(CHF)6 | -3642.54 | -5.01 | -2.93 | 2.08 | -1.72 | 1.547 | 1.523 |
| (4,0)/(CH2)8 | -4063.02 | -4.25 | -2.83 | 1.42 | -0.97 | 1.537 | 1.545 |
| (4, 0)/(CH2)4 | -3906.02 | -4.21 | -3.33 | 0.88 | 2.01 | 1.522 | 1.535 |
| (4, 0) /(CF2)8 | -5650.32 | -4.97 | -3.56 | 1.42 | 1.51 | 1.572 | 1.516 |
| (4, 0) /(CF2)4 | -4699.71 | -4.60 | -3.72 | 0.88 | 4.25 | 1.557 | 1.498 |
| (4, 0) (CHF)8 | -4856.71 | -4.61 | -3.19 | 1.41 | -2.15 | 1.548 | 1.533 |
| (5, )/(CH2)10 | -5108.70 | -4.19 | -2.84 | 1.35 | -0.68 | 1.536 | 1.563 |
| (5, 0) /(CH2)5 | -4912.50 | -4.07 | -3.33 | 0.74 | 2.34 | 1.524 | 1.538 |
| (5, 0) (CF2)10 | -7092.60 | -4.99 | -3.58 | 1.40 | 2.42 | 1.576 | 1.522 |
| (5, 0) /(CF2)5 | -5904.60 | -4.50 | -3.73 | 0.76 | 4.59 | 1.558 | 1.500 |
| (5,0)/(CHF)10 | -6100.75 | -4.53 | -3.17 | 1.36 | -3.29 | 1.540 | 1.550 |
Result and Discussion
The presence of boron and nitrogen atoms in trans position of C=C double bonds in the optimized structures of ZZ-3 (n, 0) BC2N nanotubes leads to the uniform C=C and B-N bond lengths and energetically favorable configuration for the BC2N nanotubes. The calculated C=C bond lengths (1.361-1.366 Å, compare with the 1.35 Å of H2C=CH2) are slightly shorter than normal C-C bond lengths in CNTs (1.42 Å) [47], while B-N bond lengths obtained (1.454-1.455 Å) are consistent with the reported experimental values of B–N bond lengths in the middle of the BNNTs (1.401 and 1.458Å) [48].
In order to investigate the chemical functionalization of the exterior surface of the BC2N nanotubes by carbenes, we put all of the carbenes close to the C=C bond of the BC2N nanotubes, and then it is assumed that the reaction presented in Eq. 1 is occurred. In fact, carbenes attacks to the C=C bond of the BC2N nanotubes, and a [2+1] cycloaddition takes place as follows:
(n, 0) BC2N-NT + CXY→ (n, 0) BC2N-NT/(CXY)m X, Y= H and F (1)
m= n and 2n n= 3, 4 and 5
Where (n, 0) BC2N-NT/(CXY) represents the BC2N-NT functionalized by (CH2), (CF2) and (CHF). The energies of reactions, Er, are calculated in the usual way as follows:
Er = E[BC2N-NT /(CXY)] – E[BC2N-NT] – E[CXY] (2)
where E[BC2N-NT /(CXY)] is the total energy of the complex of carbene adsorbed on a BC2N-NT and E[CXY] refers to the energy of an isolated carbene. E[BC2N-NT] is the total energy of a pristine BC2N-NT.
Among all the [2+1] cycloaddition products only (n, 0)/(CH2)2n and (n, 0)/(CHF)2n involving a fully functionalized belt around BC2N nanotube are found to have negative Er values, indicating exothermic character, while reaction energies for the other [2+1] cycloaddition reactions have positive values, indicating endothermic character. It seems that the difference between the reaction energies of [2+1] cycloaddition reactions may be due to the counteraction of the newly formed cyclopropane ring strain and the repulsion of terminated atoms of the carbenes. In order to confirm this conjecture, the geometrical characteristics of optimized structures of the [2+1] cycloaddition derivatives of the BC2N nanotubes are discussed.
The C-C bond lengths of cyclopropane in the (3, 0)/(CH2)6 are calculated to be 1.538, 1.538 and 1.533Å, which are slightly larger than normal C-C bond lengths in cyclopropane (1.51 Å) [49]. As seen in Table 1, the C-C bond lengths of cyclopropane increase with the increase of BC2N- NT tube diameter, due to the decrease in cyclopropane ring strain. On the other hand, the H…H distances of neighboring carbenes decrease with the increase of BC2N-NT tube diameter (decrease of curvature), which leads to an increase in the repulsion between the two terminated hydrogen atoms of CH2 carbenes. In this respect, as of (n, 0)/(CH2)2n, as seen in Table 1, reaction energies Er for [2+1] cycloaddition reactions decrease with an increase in the tube diameter. Hence, the DFT results indicate that tube diameter affects the [2+1] cycloaddition reaction, such that the [2+1] cycloaddition of BC2N-NTs with smaller diameter (higher curvature) is energetically more favorable. Thus, it seems that the compensation between more cyclopropane ring strain and smaller repulsion of the terminated hydrogen atoms of CH2 carbenes leads to more negative Er values for [2+1] cycloaddition reactions of narrower BC2N- NTs. Therefore, it is reasonable that replacing of hydrogen atoms with fluorine ones (difluorocarbene) and increasing of repulsion between fluorine atoms leads to the endothermic character of Er for [2+1] cycloaddition reactions. In this respect, it should be mentioned that no stable structures could be obtained for [2+1] cycloaddition reactions of CCl2 carbenes with BC2N-NTs after full geometry optimization, and half of the Cl atoms dissociate from the tube wall.
In order to remove repulsion effects between terminated atoms of carbenes, half of the carbenes are excluded and then reaction energies are recomputed using the same approach. Geometric parameters of the optimized structures of [2+1] cycloaddition derivatives, as seen in Fig. 2, reveal that the tube wall is distorted in the attached sites, such that the attached carbon atoms relax outwardly from the surface of the tube wall; the sp2 hybridization the tube surface C atom attached to the carbene changes to sp3, with an induced local structural deformation. Such structural features in the optimized geometry in the partially functionalized belt around BC2N nanotube lead to a pronounced “polygonal” cross section perpendicular to the tube axis, as shown in Fig. 2. The calculated C-C bond lengths of cyclopropane in the (n, 0)/(CH2)n are found to be shorter than those in (n, 0)/(CH2)2n, with fully functionalized belts. Therefore, it can be concluded that although removing half of the carbenes eliminates repulsion between carbenes but decrease of C-C bond lengths of cyclopropane rings increases cyclopropane ring strain and leads to endothermic character of [2+1] cycloaddition reactions.
As mentioned above, replacing of hydrogen atoms with fluorine ones increases repulsion between terminated atoms of carbenes. The positive Er values of 1.23-2.42 eV for (n, 0)/(CF2)2n and 3.42-4.59 eV for (n, 0)/(CF2)n indicate that [2+1] cycloaddition reactions are not favorable energetically based on difluorocarbene CF2 as the reactant. Therefore, in this section, in order to investigate the effect of repulsion between fluorine atoms, we replace one of the fluorine atoms
of difluorocarbenes with hydrogen atoms, see Fig. 3. It is noted that the probability of the existence of hydrogen bonding is considered when the distance between two donor-acceptor atoms is shorter than the sum of their van der Waals radii. As all the H· · ·F distances in the considered functionalized BC2N-NTs are obtained to be in the range of 1.805-2.416 Å which are shorter than the sum of the van der Waals radii of fluorine and hydrogen (2.72 Å) [50], these interactions could be considered as hydrogen bondings. Nevertheless, based on Jeffrey’s classification [51], hydrogen bondings with the bond lengths (H· · ·X) larger than 2.20 Å are considered as weak bonds.
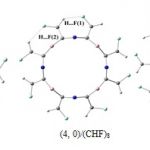 |
In terms of natural bonding orbitals (NBO) theory [52], H· · ·F hydrogen bonding can be attributed to the delocalization of electron density from the occupied lone pair of “electron donor” F (nF) into the unoccupied antibonding orbital of “electron acceptor” C–H (σ*CH) [11, 12]. The strength of these delocalization interactions, E(2), which is estimated by second-order perturbation theory, reflects the attractive interaction in the C–H· · ·F bonding and thus can be used to characterize the strength of the C-H· · ·F bond [52]. Table 2 shows that E(2) in the case of (4, 0)/(CHF)8 (RH· · ·F(1) = 2.068 Å and RH· · ·F(2) = 2.416 Å, Table 2) is 2.35 and 0.64 kcal/mol while, in the tube with increased diameters, 5.99 and 1.42 kcal/mol for the (5, 0) /(CHF)10 (RH· ·F(1) = 1.805 Å and RH· · ·F(2) = 2.159 Å, Fig. 3). It can be due to the fact that larger tubes might be better able to accommodate these functional groups involving hydrogen bondings. It is clear that the E(2), the strength of the H· · ·F hydrogen bonds, well correlates with the energy of reaction, Er, i. e. (5, 0) /(CHF)10 with stronger hydrogen bodings has more negative value for [2+1] cycloaddition reaction while in the case of (3, 0) /(CHF)6 because of higher curvature of tube sidewall only three hydrogen bondings are formed and Er increases reaching to -1.72 eV.
Electrostatic potentials are commonly used as a qualitative measure of charge distribution in molecules [53]. Murray et al. [54] in their studies suggested the molecular electrostatic potential to be a powerful tool for the analysis of a variety of chemical phenomena, in particular, the intramolecular interactions. The electrostatic surface potentials (ESP) for (3, 0)/(CHF)6, and (5, 0)/(CHF)10 are shown in Fig. 4. These electrostatic potential surface plots display the value of the electrostatic potential plotted on an isodensity surface of 0.0004 e bohr−3. As seen, the surface of the electrostatic potentials indicates the presence of two different hydrogen bonded intramolecular interaction between the electron donor and electron acceptor centers. When donor-acceptor atoms are in close proximity, by going to the larger tubes, the leaning effect along with the pyramidalization towards the lone pair orbitals of the electron acceptor center leads to cancelation of the electrostatic potential in the region between the two centers. Previous theoretical studies pointed out that the electronic structures of nanotubes can be modified in the presence of native defects, endohedral encapsulation of transition metals, heteroatom substitutions, and exohedral coating by different functional groups [55]. Therefore one purpose of the functionalizing of BC2N-NTs is to significantly modify the electronic structure of the system, especially for chemical sensors and nanobioelectronic devices [55]. The energy difference between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), Eg, indicating that pristine and functionalized BC2N-NTs have wide band gaps typical of semiconductor behavior. The band gaps of the pristine BC2N- NTs are obtained to be 0.45-0.55 eV, reasonably consistent with previous theoretical results [39]. The Eg of [2+1] cycloaddition derivatives of BC2N-NTs increases to higher energies after the functionalization. In the (n, 0)/(CH2)2n and (n, 0)/(CHF)2n models Eg increases to 1.35-2.04 eV and 1.36- 2.08 eV, respectively. Similar changes observe for the (n, 0)/(CH2)n and (n, 0)/(CHF)n models. The larger values of Eg for these structures indicates the kinetic stability of the [2+1] cycloaddition derivatives of BC2N-NTs. It is necessary to note that HOMO-LUMO gaps computed with hybrid functional are large because of the high energy of the virtual orbitals. Then we stress here that the focus is not to find precise HOMO-LUMO gaps for a given composition; instead, the primary purpose is to study the evolution and the trend of HOMO- LUMO gaps in the considered models, and this is just an approximate comparison.
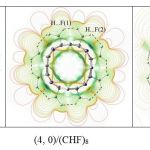 |
Table 2: NBO analysis of donor–acceptor interactions in the complexes of ZZ-3 (4, 0) BC2N nanotubes with CHF, (3, 0)/(CH2)6, (4, 0)/(CH2)8 and (5, 0)/(CH2)10 showing stabilization energy E(2) values (kcal/mol) together with Hydrogen-Bonding distances (H…F in Å).
H…F(1) H…F(2)
| RH…F | E(2) | RH…F | E(2) | |
| (3, 0) /(CHF)6 | 2.263 | 0.92 | 3.325 | – |
| (4, 0) /(CHF)8 | 2.068 | 2.35 | 2.416 | 0.64 |
| (5, 0) /(CHF)10 | 1.805 | 5.99 | 2.159 | 1.42 |
Conclusion
We have performed a computational study to investigate the functionalization of the isolated C=C units of the zigzag (n, 0) BC2N nanotubes with n =3, 4, and 5 through the [2+1] cycloaddition reactions with carbenes (CH2, CHF, and CF2). According to the DFT results we emphasize the following points. First, among all the [2+1] cycloaddition products only (n, 0)/(CH2)2n and (n, 0)/(CHF)2n involving a fully functionalized belt around BC2N nanotube have negative Er values, and reaction energies for the other [2+1] cycloaddition reactions have positive values. Difference between the reaction energies may be due to the counteraction of the newly formed cyclopropane ring strain and repulsion of terminated atoms of carbenes. Second, replacing of hydrogen atoms in CH2 carben with fluorine ones (difluorocarbene) leads to an increase in repulsion between terminated fluorine atoms whose reaction energies show the endothermic character of [2+1] cycloaddition reactions. Third, it should be mentioned that no stable structures could be obtained for [2+1] cycloaddition reactions of CCl2 carbenes with BC2N-NTs after full geometry optimization, and half of the Cl atoms dissociate from the tube wall. Forth, removing half of the carbenes eliminate repulsion between carbenes but decreases C-C bond lengths of cyclopropane rings which increases cyclopropane ring strain, leading to endothermic character of [2+1] cycloaddition reactions. Fifth, in order to further investigate the repulsion between fluorine atoms, we replace one of the fluorine atoms of difluorocarbenes with a hydrogen atom, and the probability of the existence of hydrogen bonding is considered based on geometrical parameters and natural bonding orbitals (NBO) analysis; the strength of the H· ·F hydrogen bonds, well correlates with the reaction energies. Finally, in the cases of (n, 0)/(CH2)2n absolute values of Er for [2+1] cycloaddition reactions of (n, 0) BC2N nanotubes decrease with the increase of the tube diameter, indicating that tube diameter affects the [2+1] cycloaddition, such that the [2+1] cycloaddition of BC2N-NTs with higher curvature (smaller diameter) is energetically more favorable. However, in the cases of (n, 0)/(CHF)2n larger tubes might be better able to accommodate these functional groups involving hydrogen bondings, such that (5, 0) /(CHF)10, have stronger hydrogen bodings leading to more negative Er value.
References
- Iijima, S.; Ichihashi, T.; Bando, Y.; Nature (London) 1992,356:776-778.
- Meyyappann, M.; (2004) Carbon Nanotubes Science and Applications, CRC Press.
- Close, G.F.; Yasuda, S.; Paul, B.; Fujita, S.; Wong, H.S.P.; Nano Lett. 2008,8:706-709.
- Itkis, M.E.; Yu, A.; Haddon, R.C.; Nano Lett. 2008,8:2224-2228.
- Snow, E.S.; Perkins, F.K.; Houser, E.J.; Badescu, S.C.; Reinecke, T.L.; Science 2005,307:1942-1945
- Tang, X.; Bansaruntip, S.; Nakayama, N.; Yenilmez, E.; Chang, Y.-I.; Wang, Q.; Nano Lett. 2006,6:1632-1636.
- Tasis, D.; Tagmatarchis, N.; Bianco, A.; Prato, M.; Chem. Rev. 2006,106:1105-1136.
- Wu, Y.; Phillips, J.A.; Liu, H.; Yang, R.; Tan, W.; ACS Nano 2008,2:2023-2028.
- Wong, B.S.; Yoong, S.L.; Jagusiak, A.; Panczyk, T.; Ho, H.K.; Ang, W.H.; Pastorin, G.; Adv. Drug Deliv. Rev. 2013,65:1964-2015.
- Cirillo, G.; Hampel, S.; Spizzirri,U.G.; Parisi, O.I.; Picci, N.; Iemma, F.; BioMed Res. Int. 2014,2014:825017.
- Dalili Mansour, N.; Mahboubi, F.; Nahrjou, N.; Int J Nano Dimens 2015,6:479-486.
- Ahmadi, R.; Boroushaki, T.; Ezzati, M.; Int. J. Nano. Dimens. 2015,6:19-22.
- Hirsch, A.; Angew. Chem. Int. Ed. 2002,41:1853-1859.
- Bahr, J.L.; Tour, J.M.; J. Mater. Chem. 2002,12:1952-1958.
- Banerjee, S.; Hemraj-Benny, T.; Wong, S.S.; Adv. Mater 2005,17:17-29.
- Kamaras, K.; Itkis, M.E.; Hu, H.; Zhao, B.; Haddon, R.C.; Science 2003,301:1501-1501.
- Lu, J.; Nagase, S.; Zhang, X.; Maeda, Y.; Wakahara, T.; Tsuchiya, T.; Akasaka T.; Yu, D.; Nakahodo, T.; Han, R.; Ye, H.; Gao, Z.; J. Molecular Structure: THEOCHEM 2005,725:255- 257.
- Zhao, J.; Chen, Z., Zhou, Z.; Park, H.; Schleyer, P.v.R.; Lu, J.P.; Chem. Phys. Chem. 2005,6:598-601.
- Osuna, S.; Houk, K.N.; Chem. Eur. J. 2009,15:13219-13231.
- Ghafouri, R.; Anafcheh, M.; Physica E 2014,56:351-356.
- Tagmatarchis, N.; Maigne, A.; Yudasaka, M.; Iijima, S.; Small 2006,2:490-494.
- De Volder, M.F.L.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J.; Science 2013,339: 535-539.
- Yang, N.; Chen, X. P.; Ren, T.; Zhang, P.; Yang, D.; Sens. Actuators B Chem 2015,207:690-715.
- Ohno, M.; Kojima, S.; Shirakawa, Y.; Eguchi, S.; Tetrahedron Lett 1995,36:6899-6902.
- Hirsch, A.; Synthesis 1995,1:895-913.
- Ishida, H.; Itoh, K.; Ohno, M.; Tetrahedron 2001,57:1737-1747.
- Chen, Y.; Haddon, R.C.; Fang, S.; Rao, A.M., Eklund, P.C.; Lee, W.H.; Dickey, E.C.; Grulke, E.A.; Pendergrass, J.C.; Chavan, A.; Haley, B.E.; Smalley, R.E.; J. Mater. Res. 1998,13:2423-2431.
- Lee, W.H.; Kim, S. J.; Lee, W.J.; Lee, J.G.; Haddon, R.C.; Reucroft, P.; J. Appl. Surf. Sci. 2001,181:121-127.
- Tasis, D.; Tagmatarchis, N.; Bianco, A.; Prato, M.; Chem. Rev. 2006,106:1105-1136.
- Garel, J.; Zhao, C.; Popovitz-Biro, R.; Golberg, D.; Wang, W.; Joselevich, E.; Nano Lett. 2014,14:6132-6137.
- Li, H.; Tay, R.Y.; Tsang, S.H.; Jing, L.; Zhu, M.; Leong, F.N.; Teo, E.H.T.; RSC Adv. 2017,7:12511-12517.
- Nejati, K.; Vessally, E.; Kheirollahi Nezhad, P.D.; Mofid, H.; Bekhradnia, A.; J. Phys. Chem. Solids 2017,111:238-244.
- Weng-Sieh, Z.; Cherrey, K.; Chopra, N.G.; Blasé, X.; Miyamoto, Y.; Rubio, A.; Cohen, M.L.; Louie, S.G.; Zettl, A.; Gronsky, R.; Phys. Rev. B 1995,51:11229 -11232.
- Khaleghian, M.; Azarakhshi, F.; Int. J. Nano. Dimens. 2016,7:290-294.
- Kim, S.Y.; Park, J.; Choi, H.C.; Ahn, J.P.; Hou, J.Q.; Kang, H.S.; J. Am. Chem. Soc. 2007,129:1705-1716.
- Terrones, M.; Golberg, D.; Grobert, N.; Seeger, T.; Reyes, M.R.; Mayne, M.; Kamalakaran, R.; Dorozhkin, P.; Dong, Z.C.; Terrones, H.; Rühle, M.; Bando, Y.; Adv. Mater. 2003,15:1899- 1903.
- Rupp, C.J.; Rossato, J.; Baierle, R.J.; J. Chem. Phys. 2009,130:114710-114716.
- Azevedo, S.; Eur. Phys. J. B 2005,44:203-207.
- Pan, H.; Feng, Y.P.; Lin, J.Y.; Phys. Rev. B 2006,73:035420.
- Ghafouri, R.; Anafcheh, M.; Naderi, F.; Struct. Chem. 2014,25:95-102.
- Pan, H.; Ping, Y.; Lin, F.J.; Nanoscale. Res. Lett. 2009,4:498-502.
- Anafcheh, M.; Ghafouri, R.; J. Comput. Theor. Chem. 2014,1034:32-37.
- Zhao, Y.; Truhlar, D.G.; Theor. Chem. Account. 2008,120:215-241.
- Hariharan, P.C.; Pople, J.A.; Mol. Phys. 1974,27:209-214.
- Zhang, Y.; Wu, A.; Xu, X.; Yan, Y.; J. Phys. Chem. A 2007,111:9431-9437.
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen,; J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; Windus, T.L.; Dupuis, M.; Montgomery, J.A.; J. Comput. Chem 1993,14:1347-1363.
- Zhou, Z.; Steigerwald, M.; Hybertsen, M.; Brus, L.; Friesner, R.A.; J. Am. Chem. Soc. 2004, 126:3597-3607.
- Ju, S-P.; Wang, Y-C.; Lien, T-W.; Nanoscale Res. Lett. 2011,6:160-162.
- Talaty, E.R.; Simons, G.; Theoretica chimica acta, 1977,48:331-335.
- Klein, R.A.; Chem. Phys. Lett. 2006,425:128-133.
- Jeffrey, G.A.; (1997) An Introduction to Hydrogen Bonding, Oxford University Press, Oxford.
- Reed, A.E.; Curtiss, L.A.; Weinhold, F.; Chem. Rev. 1988,88:899-926.
- Crasto1, C.J.; Stevens, E.D.; J. Molecular Structure (Theochem) 1998,54:51-59.
- Murray, J.; Seminario, J.M.; Concha, M.C.; Politzer, P.; Int. J. Quantum Chem. 1992,44:113-122.
- Saito, R.; Dressehaus, G.; Dresselhaus, M.S.; (1998) Physics Properties of Carbon Nanotubes, World Scientific, NewYork.
