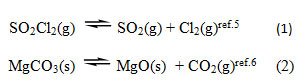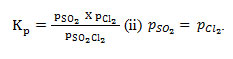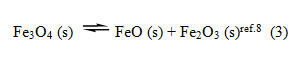The Term, “Restriction” in Phase Rule Rendered More Intelligible: A Chemical Education Article for Undergraduate Students of Chemistry in India

The Term, “Restriction” in Phase Rule Rendered More Intelligible: A Chemical Education Article for Undergraduate Students of Chemistry in India

Article Type: Article

Authors: R. Sanjeev1*, V. Jagannadham2, and R.Veda Vrath3

Abstract: We have a mathematical relation for the determination of components (C), C = C’ – rref.1 where C’ is the total number of chemical constituents or species, and r is the number of restrictions or restrictive conditions, which is seldom used and taught in Indian Universities and colleges. In this article, we have made an attempt to elaborate the term restriction, taking few examples from one of the staple engineering textbook2 in India. Even though this equation C = C’ – r appears simple, the meaning of the term r is difficult to comprehend. Therefore, we thought that elaboration of the term is of much use to both the teacher and to the taught. More importantly there appears some conceptual flaw in the calculation of components for particular reaction in this book2. And this flaw is reoccurring from the past 25 years. Our endeavor is to rectify this flaw in the interest of students, teachers and chemistry audience at large A

Address: 1Department of Chemistry, Geethanjali College of Engineerig and Technology, Keesra, Hyderabad India 2Department of Chemistry, Osmania University, Hyderabad-500007, India 3Department of Chemistry, L N Gupta Evening College, Hyderabad-500002, India Corresponding Author E-mail: rachuru1sanjeev1@rediffmail.com

Keywords: Phase; Components; Restrictions; Constituents and Phase rule

Introduction

In phase rule, components3 (C) is equal to difference between the number of chemical species in the system and the number of equations relating the concentrations of these substances in an equilibrium system. This definition is especially useful in the case of constituents, which are capable of chemical interactions.

Discussion

The meaning of the crucial sentence ‘equations relating the concentration of these substances’ in the foregoing paragraph is nothing but the restrictions imposed on the independent existence of the concentration of the substances. When the substances are related by equality, it overtly reflects that their freedom to exist independently is lost. To be more precise, equations which relate the concentration terms are nothing but intensive variables4 whose values are fixed by free energy equilibrium relations.

Let us try to comprehend the definition of components of the forgoing paragraph by taking few simple equilibrium reactions from the book2

Formula

If we consider the dissociation of SO2Cl2(g) into a evacuated vessel at a given temperature, we have two equations,  relating the concentrations of substances. These two equations are the restrictions imposed on the independent existence of the substances. (i)

Formula

Since the total number of chemical constituents are 3, the number of components is 3-2=1 (applying C = C’ – r).

Explanation of another situation is also in order:  If we start with arbitrary amounts of SO2(g) and Cl2(g), the equilibrium can be described as:

While this equilibrium follows

Formula

it fails to obey . Thus it is subjected to only one restriction. Therefore number of components in the system is 3-1 = 2. In case of equilibrium (2), there is only one equation which relates the concentrations of the substances (i.e. this equation is the restriction imposed on the independent existence of the substances) Kp = pCO2 and since the total number of chemical constituents is 3, the number of components is 3-1 = 2.

A question which often students ask, and which is not dealt in this book, is that, “Analogous to pSO2 = pCl2, why isn’t [MgO] = [CO2]? A thermodynamic property, which is an intensive variable, answers this question, the “concentration” of a solid, like its density, is an intensive property and therefore does not depend on how much of the substance, is present. For example, the “molar concentration” of copper7 (density: 8.96g/cm3) at 20oC is the same, whether we have 1 gram or 1 ton of the metal:

[Cu] = (8.96g/1 cm3) x (1 mol/63.55g) = 0.141 mol/cm3 = 141 mol/L

For this reason, the concentration of solid [MgO] is constant, and thus has nothing to do with concentration of [CO2]. Since [MgO] is not equal to [CO2], the number of equations relating to the substances is one.

Another simple equilibrium which is dealt in this book is

formula

The book says there are three chemical constituents related by one equation – the equation for equilibrium constant. Therefore the number of components is 3 -1 = 2. But this appears wrong. Since all the substances in the equilibrium are solids and since it is well known that the concentrations of pure solids9 do not appear in the equilibrium constant expression, the expression for equilibrium constant does not exist. Hence the number of components is 3 and not 2 as given in the book8.

References

  1. Elements of Physical Chemistry by S. Glasstone and D. Lewis; Second Edition pp 349; Published in India by Macmillan Company of India Ltd. ISBN 0 333 90291 2.
  2. “Chemistry in Engineering and Technology” by J C Kuriacose and V. Rajaram, Volume 1, General and Physical Chemistry; Tata McGraw-Hill Publishing Company Limited, New Delhi. Third reprint 1998.
  3. “Chemistry in Engineering and Technology” by J C Kuriacose and V. Rajaram, 376; (1), General and Physical Chemistry; Tata McGraw-Hill Publishing Company Limited, New Delhi. Third reprint 1998.
  4. Physical Chemistry by Gordon M. Barrrow, 5th Edition pp 397; Tata Mc Graw Hill edition 1992; sixth reprint 2005; ISBN 0-07-462031-2.
  5. “Chemistry in Engineering and Technology” by J C Kuriacose and V. Rajaram, 378-379;(1), General and Physical Chemistry; Tata McGraw-Hill Publishing Company Limited, New Delhi. Third reprint 1998.
  6. “Chemistry in Engineering and Technology” by J C Kuriacose and V. Rajaram,  378; (1), General and Physical Chemistry; Tata McGraw-Hill Publishing Company Limited, New Delhi. Third reprint 1998.
  7.  Chemistry by Raymond Chang, Ninth Edition Page number 610; Tata Mc Graw Hill (Special Indian Edition 2008). ISBN – 13: 978-0-07-064819-7; ISBN – 10: 0-07-064819-0.
  8. “Chemistry in Engineering and Technology” by J C Kuriacose and V. Rajaram, 379-380; (1), General and Physical Chemistry; Tata McGraw-Hill Publishing Company Limited, New Delhi. Third reprint 1998.
  9.  Chemistry by Raymond Chang Ninth Edition, 615; Tata Mc Graw Hill (Special Indian Edition 2008). ISBN – 13: 978-0-07-064819-7; ISBN – 10: 0-07-064819
218 Views
Views: 216